Главная страница / 21. Методы и технологии моделирования : 21.1. Математическая моде...
21.1. Математическая модель системы (объекта)
| ← 20.3. Контрольные вопросы и задания | 21.2. Методы математического моделирования → |
Основной этап моделирования – создание математической модели исследуемой системы. На базе математической модели анализируются характеристики системы. При компьютерном моделировании с помощью математической модели создается алгоритм программы имитации. Формальное описание объекта исследования необходимо также для взаимопонимания специалистов разных областей, объединенных для решения какой-либо глобальной задачи.
В общем случае математическую модель любой динамической системы можно представить в следующем виде [14,15]:
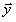 (t) = F( (t) = F(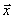 , ,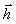 , ,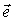 ,t), ,t), |
(21.1) |
где 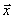 = (x1,x2,...,xn) – совокупность (вектор) входных воздействий на систему;
= (x1,x2,...,xn) – совокупность (вектор) входных воздействий на систему;
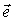 = (e1,e2,...,ek) – совокупность (вектор) случайных воздействий на систему (воз-действий внешней среды);
= (e1,e2,...,ek) – совокупность (вектор) случайных воздействий на систему (воз-действий внешней среды);
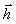 = (h1,h2,...,hm) – совокупность (вектор) внутренних параметров системы;
= (h1,h2,...,hm) – совокупность (вектор) внутренних параметров системы;
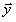 = (y1,y2,...,y5) – совокупность (вектор) выходных характеристик системы;
= (y1,y2,...,y5) – совокупность (вектор) выходных характеристик системы;
F – закон функционирования системы.
Процесс функционирования системы можно также рассматривать как последовательную смену состояний z1(t),z2(t),...,zk(t):
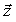 (t) = G( (t) = G(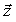 0, 0,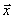 , ,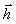 , ,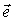 ,t), ,t), |
(21.2) |
где 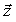 0 – совокупность начальных состояний.
0 – совокупность начальных состояний.
Таким образом, общую математическую модель системы можно представить также следующим образом:
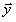 (t) = F( (t) = F(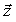 (t)). (t)). |
(21.3) |
Если модель, описывающая поведение системы, статическая, то в выражениях (21.1.–21.3.) параметр t время не вводится.
Основная задача моделирования – получение выходных характеристик системы (объекта) 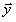 как функций от параметров
как функций от параметров 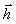 , входных переменных
, входных переменных 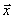 и входных воздействий на систему
и входных воздействий на систему 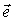 , т.е. идентификация (построение) математической модели системы (21.1.–21.3.).
, т.е. идентификация (построение) математической модели системы (21.1.–21.3.).
Для идентификации математической модели применяются различные методы моделирования.
| ← 20.3. Контрольные вопросы и задания | 21.2. Методы математического моделирования → |
