Главная страница / 4. Кодирование (представление) данных в ...: 4.2. Представление в комп...
4.2. Представление в компьютере вещественных чисел
| ← 4.1. Представление целых чисел в компьютере | 4.3. Представление в компьютере текстовой... → |
Форматы хранения вещественных чисел
Вещественные числа в математических вычислениях не имеют ограничений на диапазон и точность представления чисел. Однако в компьютерах числа хранятся в регистрах и ячейках памяти с ограниченным количеством разрядов. Поэтому точность представления вещественных чисел, представимых в машине, является конечной, а диапазон ограничен.
При написании вещественных чисел в программах вместо привычной запятой принято ставить точку. Любое вещественное число можно представить в форме записи чисел с порядком основания системы счисления.
Пример 4.4. Десятичное число 1.756 в форме записи чисел с порядком основания системы счисления можно представить так:
1,756 · 100 = 0,1756 · 101 = 0,01756 · 102 = ...
или так:
17,56 · 10-1 = 175,6 · 10-2 = 1756,0 · 10-3 = ... .
Представлением числа с плавающей точкой называется представление числа N в системе счисления с основанием q в виде:
N = m·qp,где m - множитель, содержащий все цифры числа (мантисса), p - целое число, называемое порядком.
Если плавающая точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т. е. максимальная точность представления числа в машине.
Если в мантиссе первая цифра после точки (запятой) отлична от нуля, то такое число называется нормализованным.
Мантиссу и порядок q-ичного числа принято записывать в системе с основанием q, а само основание — в десятичной системе.
Пример 4.5. Приведем примеры нормализованного представления числа в десятичной системе:
2178,01 = 0,217801 · 104
0,0045 = 0,45 · 10-2
Примеры в двоичной системе:
10110,01 = 0,1011001 · 2101 (порядок 1012 = 510)
Современными компьютерами поддерживаются несколько международных стандартных форматов хранения вещественных чисел с плавающей точкой, различающихся по точности, но все они имеют одинаковую структуру. Вещественное число хранится в трех частях: знак мантиссы, смещенный порядок и мантисса:
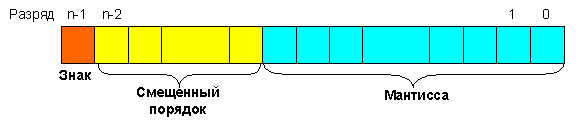
Смещенный порядок n-разрядного нормализованного числа вычисляется следующим образом: если для задания порядка выделено k разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2k-1 - 1).
Таким образом, порядок, принимающий значения в диапазоне от -128 до +127, преобразуется в смещенный порядок в диапазоне от 0 до 255. Смещенный порядок хранится в виде беззнакового числа, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.
Количество разрядов, отводимых под порядок, влияет на диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате. Очевидно, что чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. В связи с тем, что у нормализованных вещественных чисел старший бит мантиссы всегда равен 1, этот старший бит не хранится в памяти.
Любое двоичное целое число, содержащее не более m разрядов, может быть без искажений преобразовано в вещественный формат.
Таблица 4.3. Стандартные форматы представления вещественных чисел
| Формат |
Что хранится |
Кол-во битов, отводимых под смещенный порядок |
Кол-во битов, отводимых под мантиссу |
|---|---|---|---|
| Одинарный |
32-разрядное нормализованное число со знаком | 8 |
23 |
| Двойной |
64-разрядное нормализованное число со знаком | 11 |
52 |
| Расширенный |
80-разрядное число со знаком (возможно ненормализованные) | 15 |
64 |
Пример 4.6. Представление нормализованных чисел в одинарном формате.
Проиллюстрируем, как будет храниться число 37,1610. При переводе в двоичное число не получается точного перевода: 100101,(00101000111101011100) - дробная часть, заключенная в скобках, повторяется в периоде.
Переводим число в нормализованный вид:
0,100101(00101000111101011100) · 2110
Представим вещественное число в 32-разрядном формате:
- Знак числа «+», поэтому в знаковый разряд (31) заносим 0.
- Для задания порядка выделено 8 разрядов, к истинному значению порядка, представленного в дополнительном коде, прибавляем смещение (27 - 1) = 127. Так как порядок положительный, то прямой код порядка совпадает с дополнительным, вычислим смещенный порядок: 00000110 + 01111111 = 10000101. Заносим полученный смещенный порядок.
- Заносим мантиссу, при этом старший разряд мантиссы убираем (он всегда равен 1).
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Знак | Смещенный порядок | Мантисса | |||||||||||||||||||||||||||||
В данном примере мы смогли перенести только 24 разряда, остальные были утеряны с потерей точности представления числа.
| ← 4.1. Представление целых чисел в компьютере | 4.3. Представление в компьютере текстовой... → |
