Главная страница / 23. Алгоритм и его свойства. Способы зап...: 23.3. Данные алгоритмов

23.3. Данные алгоритмов

← 23.2. Свойства алгоритма 23.4. Элементарные алгоритмические действия →

Как уже было сказано выше, алгоритм оперирует с данными. Он преобразует входные данные в выходные, образуя в этом процессе промежуточные данные. Данные могут быть простые и сложные (структурированные). Простые данные представляют собой переменные и константы. Константа – это величина, имеющая постоянное значение, не изменяющееся в процессе работы алгоритма. Переменная – это величина, способная изменять свое значение и обладающая следующими свойствами:

  • переменная обязательно должна иметь идентификатор – имя, по которому к ней производится обращение;
  • переменная должна иметь определенный тип;
  • переменной может быть присвоено значение ее типа;
  • если переменной не присвоено значение, то она является неинициализированной и пользоваться ее значением нельзя;
  • если переменной присвоено значение, она хранит его до тех пор, пока ей не будет присвоено другое;
  • значение переменной можно получать от нее многократно - при этом оно сохраняется.

Константы и переменные алгоритмов могут быть числового и символьного типов. Данные числового типа могут хранить числовые значения. Так как целые и вещественные числа представляются в компьютерной обработке принципиально по-разному, для числовых данных необходимо определять подтип – целые, вещественные или комплексные.  Данные символьного типа могут хранить в себе коды символов, используемых при кодировании нечисловой информации. Отдельно следует выделить логический тип – данные этого типа могут иметь два значений – Истина (true, логическая единица) и Ложь (false, логический ноль), образующие полное множество.

Сложные (структурированные) типы данных строятся из простых. Это, прежде всего, массивы.

Массив – это совокупность переменных одного типа, имеющих один и тот же идентификатор и различающихся между собой одним или несколькими индексами.

В самом простом случае индекс представляет собой порядковый номер элемента массива. Число индексов определяет «мерность» массива. Одномерный числовой массив соответствует математическому понятию вектор, а двумерный числовой – понятию матрица. Одномерный символьный массив обычно называется строка, а двумерный символьный – текст. Число индексов элементов массивов не ограничивается, хотя в практических задачах обычно не превосходит трех - четырех.

Другим сложным типом данных является структура или запись.

Структура – это совокупность переменных разных типов, имеющих различные идентификаторы.

Идентификатор элемента структуры состоит из двух частей, разделенных точкой, – идентификатора структуры и идентификатора собственно элемента. Например, murka.tau – переменная tau структуры murka.

В качестве элементов массивов или структур могут использоваться другие массивы или структуры.

Существуют и другие сложные типы данных: множества, объекты классов и пр., которые в данном разделе не рассматриваются.

Перед разработкой алгоритма должна быть выполнена разработка структуры входных и выходных данных. Она заключается в определении состава входных и выходных данных, определении их типов и присвоении им идентификаторов. Например, для алгоритма решения квадратного уравнения ax2 + bx + c = 0 входными данными могут являться переменные a, b и с, имеющие вещественный числовой тип и соответствующие одноименным коэффициентам уравнения. С выходными данными здесь несколько сложнее. Так как уравнение может иметь как вещественные, так и комплексные корни, то одним из вариантов решения может быть следующая структура выходных данных:

  • x1 – первый вещественный корень или вещественная часть комплексно сопряженных корней;
  • x2 – второй вещественный корень или мнимая часть комплексно сопряженных корней;
  • key – ключ типа корней – вещественные или комплексно сопряженные.

Переменные x1  и x2 имеют вещественный числовой тип, а переменная key  может быть логической или числовой переменной с предварительно установленной кодировкой значений, например:

  • key = 0 – вещественные корни;
  • key = 1 – комплексно сопряженные корни.

Для алгоритма решения системы линейных алгебраических уравнений 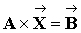formula1 структура входных и выходных данных может быть следующей:

  1. Входные переменные:
    • A – двумерный вещественный массив матрицы коэффициентов системы;
    • B – одномерный вещественный массив вектора свободных членов.
  2. Выходные переменные:
    • X – одномерный вещественный массив вектора неизвестных;
    • Err – переменная целого типа – код ошибки, сигнализирующий об успешном или неуспешном завершении алгоритма.

Входные и выходные данные алгоритма иногда удобно изобразить на структуре «черного ящика» (black box). На рис. 23.1 показана структура внешних данных алгоритма вычисления корней квадратного уравнения. На структуре указаны типы переменных: Real – вещественный и Int – целый.

← 23.2. Свойства алгоритма 23.4. Элементарные алгоритмические действия →