Главная страница / 5. Основные понятия алгебры логики: 5.2. Логические операции:...
5.2. Логические операции: инверсия, дизъюнкция и конъюнкция
| ← 5.1. Логические величины: истина (логическая... | 5.3. Основные законы булевой алгебры → |
Алгебра логики рассматривает любое высказывание только с одной точки зрения — истинно оно или ложно.
Заметим, что зачастую трудно установить истинность высказывания. Так высказывание «Площадь поверхности Индийского океана равна 75 млн км2» в одной ситуации можно считать ложным, а в другой — истинным. Ложным — так как указанное значение неточное и вообще не постоянное. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.
Употребляемые в обычной речи слова и словосочетания не, и, или, если... , то, тогда и только тогда и др. позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Так из элементарных высказываний «Петров — врач», «Петров — шахматист» при помощи связки и можно получить составное высказывание «Петров — врач и шахматист», понимаемое как «Петров — врач, хорошо играющий в шахматы».
При помощи связки или из этих же высказываний можно получить составное высказывание «Петров — врач или шахматист», понимаемое в алгебре логики как «Петров или врач, или шахматист, или и врач и шахматист одновременно».
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
НЕ. Операция, выражаемая этим словом, называется отрицанием и обозначается чертой над высказыванием (или знаком 
).
Высказывание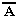 
истинно, когда A ложно, и ложно, когда A истинно. Например, «Луна — спутник Земли» (А); «Луна — не спутник Земли» ().
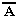Схема НЕ (инвертор) реализует операцию отрицания.
Если на входе схемы 0, то на выходе 1; если на входе 1, на выходе 0. Условное обозначение инвертора — на рис. 5.1, а таблица истинности — в табл. 5.1.
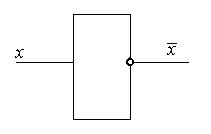
Рис. 5.1. Условное обозначение инвертора
Талица 5.1. Таблица истинности инвертора
| А | Не А |
|---|---|
| Да (1) | Нет (0) |
| Нет (0) | Да (1) |
И. Операция, выражаемая этой связкой, называется конъюнкцией (лат. conjunctio — соединение), или логическим умножением, и обозначается точкой « . » (может также обозначаться знаками ^ или &).
Высказывание А · В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание «10 делится на 2 и 5 больше 3» истинно, а высказывания «10 делится на 2 и 5 не больше 3», «10 не делится на 2 и 5 больше 3», «10 не делится на 2 и 5 не больше 3» — ложны.
Схема И реализует конъюнкцию двух или более логических значений.
Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 5.2, таблица истинности конъюнкции — в табл. 5.2.
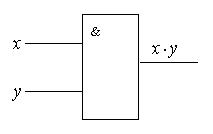
Рис. 5.2. Условное обозначение схемы И с двумя входами
Талица 5.2. Таблица истинности схемы И с двумя входами
| А | В | А и В |
|---|---|---|
| Да (1) | Да (1) | Да (1) |
| Да (1) | Нет (0) | Нет (0) |
| Нет (0) | Да (1) | Нет (0) |
| Нет (0) | Нет (0) | Нет (0) |
ИЛИ. Операция, выражаемая этой связкой (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом).
Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание «10 не делится на 2 или 5 не больше 3» ложно, а высказывания «10 делится на 2 или 5 больше 3», «10 делится на 2 или 5 не больше 3», «10 не делится на 2 или 5 больше 3»— истинны.
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.
Условное обозначение схемы ИЛИ представлено на рис. 5.3, таблица истинности — в табл. 5.3.
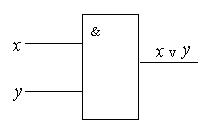
Рис. 5.3. Условное обозначение схемы ИЛИ с двумя входами
Талица 5.3. Таблица истинности схемы ИЛИ с двумя входами
| А | В | А или В |
|---|---|---|
| Да (1) | Да (1) | Да (1) |
| Да (1) | Нет (0) | Да (1) |
| Нет (0) | Да (1) | Да (1) |
| Нет (0) | Нет (0) | Нет (0) |
Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (НЕ), затем конъюнкция (И), после конъюнкции — дизъюнкция (ИЛИ) и в последнюю очередь — импликация.
| ← 5.1. Логические величины: истина (логическая... | 5.3. Основные законы булевой алгебры → |