Главная страница / 3. Системы счисления: 3.3. Перевод чисел из дес...
3.3. Перевод чисел из десятичной системы в другую позиционную систему счисления и обратно
| ← 3.2. Двоичная, восьмеричная и... | 3.4. Арифметические операции в позиционных... → |
Навигация по разделу:
- 3.3.1. Перевод целого десятичного числа в другую позиционную систему счисления
- 3.3.2. Перевод правильной десятичной дроби в другую позиционную систему счисления
- 3.3.3. Перевод числа в десятичную систему счисления
3.3.1. Перевод целого десятичного числа в другую позиционную систему счисления
Правило перевода целого десятичного числа N в систему счисления с основанием q.
Необходимо N разделить с остатком («нацело») на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q и т.д., пока последнее полученное неполное частное не станет равно нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения [2].
Пример 3.2. Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
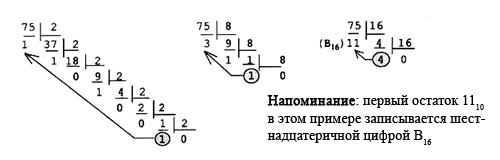
Ответ: 7510 = 10010112 = 1138 = 4B16.
3.3.2. Перевод правильной десятичной дроби в другую позиционную систему счисления
Правило перевода правильной десятичной дpоби F в систему счисления с основанием q.
Необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой [2].
Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q-(k+1)/ 2.
Пример 3.3. Переведем число 0,42 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
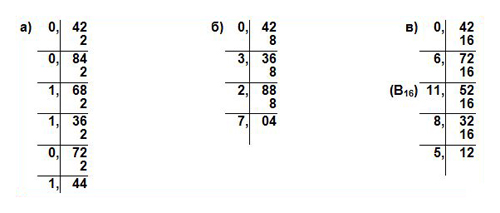
Ответ:
а) 0,4210= 0,011012 с предельной абсолютной погрешностью 2-6/2=2-7;
б) 0,4210=0,3278 с предельной абсолютной погрешностью 8-4/2=2-13;
в) 0,4210=0,6B852 с предельной абсолютной погрешностью 16-5/2=2-21.
Для чисел, имеющих целую и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для каждой из частей, а затем складываются.
3.3.3. Перевод числа в десятичную систему счисления
Правило перевода в десятичную систему числа X, записанного в q-ичной системе счисления в виде Xq = (an an-1 ...a0 , a-1 a-2 ... a-m)q производится путем вычисления значения многочлена:
X10 = an qn + an-1 qn-1 + ... + a0 q0 + a-1 q-1 + a-2 q-2 + ... + a-m q-m ,
здесь n – номер разряда (считается от запятой влево начиная с 0); m – номер разряда дробной части (считается вправо от запятой, начиная с 1).
Пример 3.4.
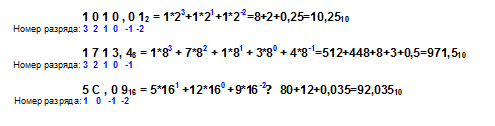
| ← 3.2. Двоичная, восьмеричная и... | 3.4. Арифметические операции в позиционных... → |
