Главная страница / 23. Алгоритм и его свойства. Способы зап...: 23.4. Элементарные алгори...
23.4. Элементарные алгоритмические действия
| ← 23.3. Данные алгоритмов | 23.5. Способы записи алгоритмов → |
Алгоритм строится из структурных конструкций и элементарных алгоритмических действий, к которым относятся присваивание, ввод и вывод данных, а также обращение к вспомогательному алгоритму.
Присваивание может быть представлено в виде
var := <выражение> или <выражение> → var,
где var – условный идентификатор переменной.
Выражение – это синтаксически правильная конструкция, состоящая из операндов (переменных и констант), знаков операций между ними, вызовов функций, скобок.
Все переменные, входящие в выражение, должны иметь определенные значения, действия, выполняемые над операндами, должны быть корректны, а функции – определены. При этом выражение будет иметь значение определенного типа, которое вычисляется и присваивается переменной var.
Если операнды – числовые величины, то над ними можно выполнять известные математические действия: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. В выражении могут быть использованы известные алгебраические функции: абсолютной величины, синуса, экспоненты, логарифма и т.п.
Над операндами логического типа можно выполнять операции отрицания (инверсии, НЕ, NOT), логического сложения (дизъюнкции, ИЛИ, OR) и логического умножения (конъюнкции, И, AND).
Данные символьного типа обычно используются в качестве аргументов функций, специально предназначенных для работы с ними.
Алгоритмическое действие ввод значения представляет собой еще один способ присвоения значения переменной, при котором это значение вводится с консоли (клавиатуры, файла или другого канала). Условно его можно обозначить как Input(var), где var – идентификатор переменной, которой присваивается значение.
Противоположное действие вывод значения заключается в выводе значения переменной var на консоль (монитор, файл, канал) – Output(var).
Самым сложным алгоритмическим действием является обращение к вспомогательному алгоритму. Его лучше пояснить на конкретном примере. Пусть при выполнении основного алгоритма возникла необходимость решения квадратного уравнения s*t2 + q*t + r = 0 (корни уравнения – вещественные). Предположим, что алгоритм решения квадратного уравнения со структурой входных и выходных данных, представленных на рис. 23.1, уже имеется. Тогда, в нужный момент, его можно вызвать, передав в него входные данные. Алгоритм Root2 исполнится и передаст в вызвавший его основной алгоритм выходные данные. Схема взаимодействия основного и вспомогательного алгоритмов представлена на рис. 23.2. При вызове алгоритма Root2 переменная s основного алгоритма передаст свое значение переменной a вспомогательного. Аналогично произойдет передача значений: q → b и r → c. После завершения работы вспомогательного алгоритма произойдет передача его выходных данных переменным основного алгоритма: x1 → t1 и x2 → t2.
Кроме элементарных алгоритмических действий при построении алгоритмов используются структурные конструкции: следование, бинарное ветвление, множественное ветвление и циклы, которые рассматриваются ниже.
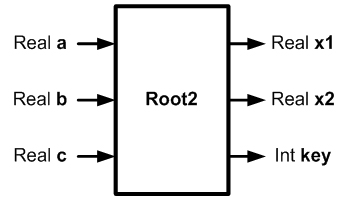
Рис.23.1. Структура входных и выходных данных алгоритма решения квадратного уравнения
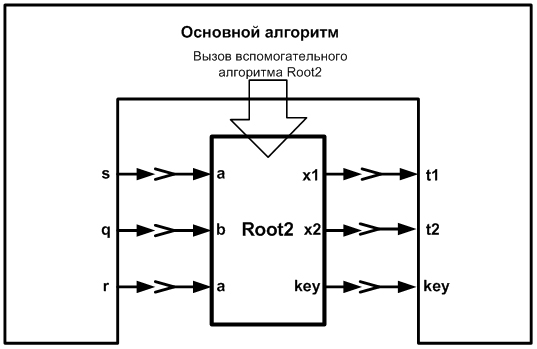
Рис. 23.2. Схема передачи данных при вызове вспомогательного алгоритма
| ← 23.3. Данные алгоритмов | 23.5. Способы записи алгоритмов → |
