Главная страница / 24. Базовые алгоритмические структуры: 24.2. Разветвляющая алгор...
24.2. Разветвляющая алгоритмическая структура
| ← 24.1. Линейная алгоритмическая структура | 24.3. Циклические алгоритмические структуры → |
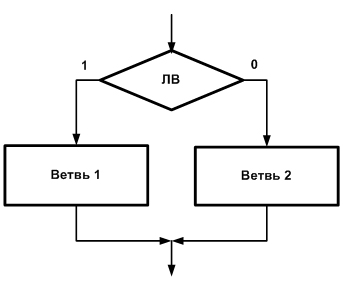
Разветвляющая алгоритмическая структура представляет собой конструкцию, состоящую из двух или более ветвей. Наиболее простой ее вариант – бинарное ветвление (альтернатива, структура if-else, если-то-иначе). Ее блок-схема представлена на рис. 24.3, а, а псевдокод – следующим текстом:
…
если <логическое выражение>
то Ветвь 1
иначе Ветвь 2
все
…При ее выполнении сначала вычисляется логическое выражение. Если оно имеет значение Истина, то выполняется ветвь A, если же Ложь – то ветвь B. Каждая ветвь может включать в себя одно или несколько элементарных действий. Если в ветвь входит несколько действий (операторов), то их необходимо объединить в одно составное действие с помощью служебных слов нач и кон (см. пример алгоритма решения квадратного уравнения в гл. 23). На блок-схеме бинарное ветвление изображается в виде ромбовидного графического элемента альтернатива. Направления перехода могут помечаться также 1 или да (истина) и 0 или нет (ложь).
Частным случаем бинарного ветвления является обход, при котором в случае равенства логического выражения значению Ложь не должно выполняться никакого действия – ветвь пустая.
…
если <логическое выражение>
то Ветвь 1
все
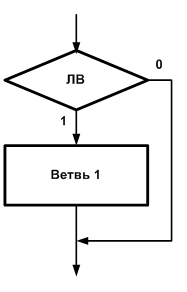
…Блок-схема этой структуры приведена на рис. 24.3, б.
 |
 |
| a | б |
Рис. 24.3. Блок-схема структур «ветвление» (а) и «обход» (б)
В качестве логического выражения может быть использовано выражение отношения (условие), в котором два выражения сравниваются знаками отношения, например, k = 0 или i < n или sin(x + π/2)>
Множественное ветвление представляет собой структуру, разветвляющуюся на более чем две ветви. С точки зрения теоретического программирования она является избыточной, так как может быть реализована с помощью бинарных ветвлений. Но практически все языки программирования имеют оператор, поддерживающий эту структуру, поэтому рассмотрим ее на примере ветвления на четыре ветви (блок-схема на рис. 24.4). Ветвлением управляет выражение-селектор s, которое может принимать предусмотренные значения a, b и c. Если s = a, то выполняется ветвь A, если s = b, то выполняется ветвь B, и если s = с, то выполняется ветвь С. В структуре также имеется ветвь X, которая будет выполняться, если селектор s примет не предусмотренное для исполнения предыдущих ветвей значение.
На рис. 24.5 показана реализация этой структуры с помощью бинарных ветвлений.
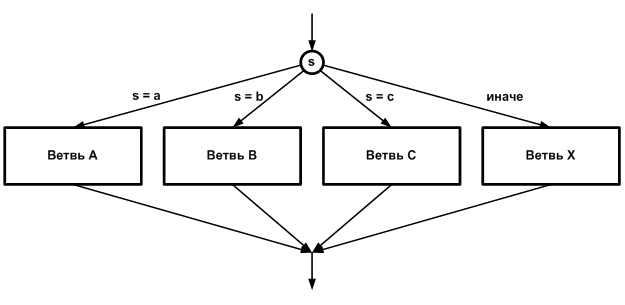
Рис. 24.4. Блок-схема множественного ветвления
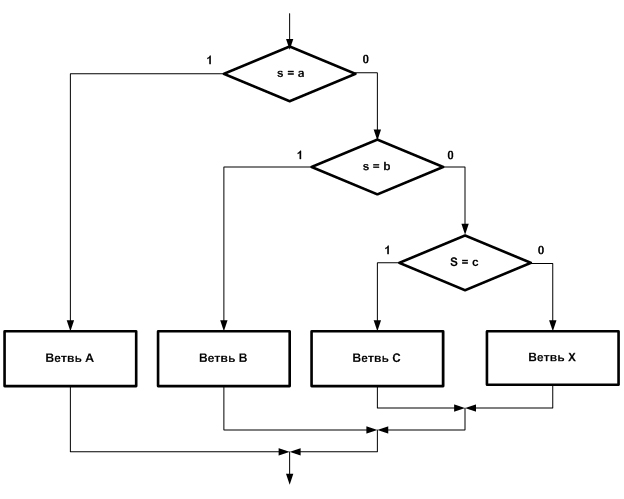
Рис. 24.5. Реализация множественного ветвления с помощью бинарных ветвлений
На псевдокоде множественное ветвление записывается следующим образом:
выбор
при s = a: Ветвь A
при s = b: Ветвь B
при s = c: Ветвь C
иначе Ветвь X
все
| ← 24.1. Линейная алгоритмическая структура | 24.3. Циклические алгоритмические структуры → |
