Главная страница / 21. Методы и технологии моделирования : 21.2. Методы математическ...
21.2. Методы математического моделирования
| ← 21.1. Математическая модель системы (объекта) | 21.3. Технология математического... → |
Методы моделирования, решающие задачу идентификации математической модели, можно разделить на четыре основные группы: аналитические, численные, имитационные, вероятностно-статистические [4],[9],[10],[14],[15],[16],[17].
Исторически первыми были разработаны аналитические методы моделирования и сложился аналитический подход к исследованию систем.
Аналитические методы моделирования. Аналитические методы позволяют получить характеристики системы как некоторые функции параметров ее функционирования. Таким образом, аналитическая модель представляет собой систему уравнений, при решении которой получают параметры, необходимые для оценки системы (время ответа, пропускную способность и т.д.).
Пример 1. Модель, описывающая путь S(t), пройденный автомобилем при равноускоренном движении с момента начала движения:
| S(t) = ν0t + at2, | (21.4) |
где ν0, a – начальная скорость и ускорение.
Для того чтобы вычислить значение S(t) в заданный момент времени t достаточно подставить конкретные значения ν0 и a в уравнение (21.4) и выполнить аналитический расчет S(t) .
Пример 2. Процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением:
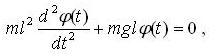 |
(21.5) |
где m, l – масса и длина подвеса маятника;
g – ускорение свободного падения;
φ(t) – угол отклонения маятника в момент времени t.
Из этого уравнения свободного колебания маятника можно найти точные значения интересующих характеристик с помощью аналитических методов решения дифференциальных уравнений.
Пример 3. Небольшое предприятие может выпускать продукцию двух типов, прибыль от реализации единицы продукции первого типа составляет 600 у.е., второго типа – 500 у.е. Для изготовления единицы продукции первого типа необходимо затратить 10 единиц материала, трудовые ресурсы – 5 чел./час.; второго типа – 7 ед. материала, трудовые ресурсы – 4 чел./ч. Общие ресурсы предприятия на планируемый период: 1000 ед. материала, 800 чел./ч. Определить оптимальный план выпуска продукции, максимизирующий прибыль предприятия.
Данная задача относится к классу оптимизационных (задача целочисленного линейного программирования). Математическая модель задачи имеет следующий вид:
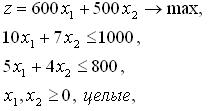 |
(21.6) |
где x1,x2 – количество единиц продукции соответственно первого и второго типов.
Решается эта задача аналитически с помощью симплекс-метода. В результате решения точно определяются оптимальные значения x1,x2 и прибыль предприятия z.
Достоинство аналитических методов: высокая точность вычислений.
Недостатки аналитических методов:
- разработаны только для узкого класса моделей, задач;
- при выводе формул, на которых эти методы основываются и которые используются для расчета интересующих параметров, необходимо принять определенные допущения и упростить модель. Например, уравнение (21.4) описывает движение автомобиля в идеальных условиях: отсутствие сопротивления воздуха, трения и т.п.
Смена состояний реальной системы (объекта) происходит под воздействием множества как внешних, так и внутренних факторов, подавляющее большинство которых носит стохастический характер. Вследствие этого, а также из-за большой сложности большинства реальных систем применение аналитических методов ограничено.
При аналитическом моделировании компьютер используется в качестве вычислителя по аналитическим зависимостям. Разработаны пакеты прикладных программ, в которых реализованы аналитические методы решения систем алгебраических, дифференциальных, интегральных уравнений; методы решения оптимизационных задач. Например, Mathlab, Maple, MathCard.
Численные методы моделирования. Математическая модель также представляет собой систему линейных, нелинейных уравнений, но решается система уравнений методами вычислительной математики. Все численные методы предполагают итерационное решение задачи. На нулевой итерации задается начальное решение (приближение) и оценивается его точность, на последующих итерациях начальное приближение последовательно уточняется. Итерационный процесс продолжается до тех пор, пока не будет достигнута заданная точность решения, не будет выполнен заданный критерий останова.
Пример 4. Численный метод бисекций (деления отрезка пополам) применяется для решения алгебраических и трансцендентных уравнений следующего вида: f(x)=0, причем f(x) – непрерывная функция [9].
Суть метода сводится к следующему: задается начальное приближение корня (x0) на отрезке [a, b]. Точка x0 разбивает отрезок на две равные части: [a, x0] и [x0, b]. Исходный отрезок [a, b] удовлетворяет условию: f(a)f(b)<0. Тогда согласно теореме Больцано–Коши внутри отрезка [a, b] существует точка c, в которой значение функции равно нулю, т.е. f(с) = 0, с ∈ [a, b]. Далее вычисляются значения функции на концах отрезков [a, x0] и [x0, b] и находится отрезок, на концах которого функция принимает значения разных знаков. Именно этот отрезок на следующей итерации делится пополам. Процесс построения последовательности отрезков позволяет найти ноль функции f(x) (корень уравнения f(x) = 0) с любой заданной точностью [6].
Опишем один шаг итераций. Пусть на(n-1)-м шаге найден отрезок [an-1, bn-1]⊂[a, b], такой, что f(an-1)f(bn-1 )<0. Делим его пополам точкой ξ = (an-1 + bn-1)/2 и вычисляем f(ξ). Если f(ξ) = 0, то ξ = (an-1 + bn-1)/2 – корень уравнения. Если f(ξ) ≠ 0, то из двух полученных отрезков выбираем тот, на концах которого функция имеет противоположные знаки, так как корень уравнения принадлежит этому отрезку. Таким образом,
|
an = an-1, bn = ξ, если f(ξ)f(an-1) < 0, an = ξ, bn = bn-1, если f(ξ)f(an-1) > 0. |
(21.7) |
Если требуется найти корень с точностью до ξ, то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 2ξ. Тогда координата середины отрезка и есть значение корня с требуемой точностью ξ.
Разработаны численные методы для решения нелинейных уравнений (метод бисекций, метод простых итераций, метод Ньютона, метод Чебышева, метод Данко и т.д.), систем нелинейных уравнений (метод простых итераций, метод Ньютона, метод наискорейшего спуска и т.д.), решения задачи поиска минимума нелинейной функции (метод градиентного спуска, метод Нелдера–Мида и т.д.).
Класс задач, которые решаются численными методами, значительно шире. Численные методы не дают точных решений, но позволяют задать любую степень точности решения. Использование численных методов оправдано, когда аналитические методы не существуют, например, математическая модель описывается слишком сложным нелинейным уравнением или системой нелинейных уравнений.
Численные методы, как и аналитические, реализованы в пакетах прикладных программ, например Mathlab, Maple, MathCard.
Имитационные методы моделирования [5]. С развитием вычислительной техники широкое применение получили имитационные методы моделирования для анализа систем, преобладающими в которых являются стохастические воздействия.
Суть имитационного моделирования заключается в имитации процесса функционирования системы во времени, с соблюдением таких же соотношений длительности операций, как и в системе оригинале. При этом имитируются элементарные явления, составляющие процесс; сохраняется их логическая структура, последовательность протекания во времени. Результат имитационного моделирования – получение оценок характеристик системы.
Известный американский ученый Роберт Шеннон дает следующее определение [17]: «Имитационное моделирование – процесс конструирования модели реальной системы и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить (в рамках ограничений, накладываемых некоторым критерием или совокупностью критериев) различные стратегии, обеспечивающие функционирование данной системы».
Все имитационные модели используют принцип черного ящика. Это означает, что они выдают выходной сигнал системы при поступлении в нее некоторого входного сигнала. Поэтому в отличие от аналитических методов для получения результатов необходимо осуществлять «прогон» имитационных моделей, т.е. подачу некоторой последовательности сигналов, объектов или данных на вход модели и фиксацию выходной информации, а не «решать» их. Происходит своего рода «выборка» состояний объекта моделирования (состояния – свойства системы в конкретные моменты времени) из пространства (множества) состояний (совокупность всех возможных значений состояний). Насколько репрезентативной окажется эта выборка, настолько результаты моделирования будут соответствовать действительности. Этот вывод показывает важность применения вероятностно-статистических методов оценки результатов имитации.
В процессе имитационного моделирования используется метод статистического моделирования, который первоначально развивался как метод статистических испытаний (Монте-Карло). Это численный метод, состоящий в получении оценок вероятностных характеристик, совпадающих с решением аналитических задач (например, с решением уравнений или вычислением определенного интеграла). Впоследствии этот метод стал применяться для имитации процессов, происходящих в системах, внутри которых есть источник случайности или которые подвержены случайным воздействиям.
Методы имитационного моделирования широко применяются при исследовании систем массового обслуживания.
Под системой массового обслуживания (СМО) понимают динамическую систему, предназначенную для эффективного обслуживания потока заявок (требований на обслуживание) при ограничениях на ресурсы системы. Под это определение подходит значительная часть реальных систем, которые нас окружают: библиотека, аэропорт, больница, университет, вычислительная система, производственная система и т.д.
Пример 5. В качестве примера СМО приведем информационно-поисковую систему. Система включает распределенный банк данных, организованный на базе трех удаленных друг от друга вычислительных центров А, В и С. Все центры связаны между собой каналами передачи информации, работающими в дуплексном режиме независимо друг от друга. В каждый из центров поступают заявки на проведение информационного поиска, где они предварительно обрабатываются, в результате чего формируются запросы для центров А, В и С. В центре, получившем заявку от пользователя, начинается поиск информации по запросу, а на другие центры по соответствующим каналам передаются тексты запросов, после чего там также может начаться поиск информации. Тексты ответов передаются соответствующим каналом в центр, получивший заявку на поиск. Заявка считается выполненной, если получены ответы от всех трех центров.
Необходимо рассчитать характеристики эффективности функционирования информационно-поисковой системы: число заявок, поступивших и обслуженных в каждом центре; вероятность загрузки компьютеров центров; характеристики очереди запросов к компьютерам каждого центра; среднее время обслуживания заявок в каждом центре и т.д.
Характерным для приведенной задачи и для других подобных задач из различных предметных областей являются:
- условие двойной случайности: случайный момент времени поступления заявки на обслуживание (в информационно-поисковую систему, на телефонную станцию, на пункт скорой помощи, на вход процессора и т.д.); случайная длительность времени обслуживания;
- наличие очередей (задач к компьютерам вычислительного центра, судов перед шлюзами, деталей на обработку и т.д.).
Решение задачи имитационным методом предполагает розыгрыш интервалов между поступлением заявок на информационный поиск в центры А, В и С и интервалов обслуживания заявок, согласно заданному закону; вычисление моментов прихода заявок в систему и окончания обслуживания заявок; вычисление для каждой заявки ее времени ожидания в очереди на обслуживание и простоя системы (в ожидании заявки). Составляются алгоритм и компьютерная программа, которые имитируют работу СМО либо в течение заданного промежутка времени, либо по обслуживанию заданного количества заявок. Результат работы программы: оценка характеристик эффективности функционирования системы (среднее время ожидания заявок в очереди, вероятность простоя и т.д.).
Применение имитационных методов моделирования целесообразно при выполнении определенных условий [17].
- Не существует законченной математической постановки данной задачи либо еще не разработаны аналитические методы решения сформулированной математической модели. К этой категории относятся многие модели массового обслуживания, связанные с рассмотрением очередей.
- Аналитические методы имеются, но математические процедуры столь сложны и трудоемки, что имитационное моделирование дает более простой способ решения задачи.
- Кроме оценки определенных характеристик системы, необходимо осуществить на имитационной модели наблюдение за ходом процесса в течение определенного периода.
Дополнительным преимуществом имитационного моделирования можно считать широкие возможности его применения в сфере образования и профессиональной подготовки. Использование имитационной модели позволяет экспериментатору видеть и «разыгрывать» на модели реальные процессы и ситуации.
Достоинства имитационных методов: применение для решения широкого класса задач, возможность учесть при моделировании любые стохастические воздействия на систему.
Недостатки имитационных методов: низкая точность по сравнению с аналитическими методами; невозможность задать требуемую точность решения, как в численных методах.
На рынке программных продуктов широко представлено программное обеспечение, реализующее имитационные методы моделирования. К нему относятся среды имитационного моделирования GPSS, SimScript, Simula, Arena, Extend, AveSim, AnyLogic и др.; программные комплексы, специализирующиеся на моделировании узкого круга систем одной конкретной предметной области. Например, пакеты имитационного моделирования производственных систем (AutoMod, WITNESS, QUEST, ProModel и др.); пакеты имитационного моделирования для медицинских учреждений (MedModel); пакеты имитационного моделирования сетей связи (COMNET, OPNET Modeler, IT Decision Guru).
Вероятностно-статистические методы моделирования. Применяются для описания зависимостей между выходными характеристиками системы и ее входными переменными (параметрами), в случае если эти зависимости [4]:
- стохастичны по своей природе, т.е. позволяют устанавливать лишь вероятностные логические соотношения изучаемых событий А и В, а именно соотношения типа «из факта осуществления события А следует, что событие В должно произойти, но не обязательно, а лишь с некоторой вероятностью р;
- выявляются на основании выборочных данных статистического наблюдения за анализируемыми событиями или переменными.
Пример 6. Исследуется зависимость между прибылью предприятий отрасли (y) и объемом производства (x1), фондом заработной платы (x2). Имеются исходные данные по 100 предприятиям отрасли за прошедший год. Простейшая модель взаимосвязи показателей описывается статистической линейной моделью (моделью линейной регрессии):
| y = ax1 + bx2 + c + ε, | (21.8) |
где a, b, c – параметры модели;
ε – случайный остаток.
Параметры модели оценивается на основе использования вероятностно-статистических методов (методов регрессионного анализа). Случайный остаток отражает влияние на y неучтенных факторов и/или ошибок измерений. В результате применения модели можно спрогнозировать среднюю прибыль предприятия отрасли при заданных значениях объема производства и фонда заработной платы (например, на следующий год) с некоторой вероятностью р.
Вероятностно-статистические методы широко используются при обработке результатов, полученных имитационными методами моделирования, в ходе имитационного эксперимента, как отмечалось выше.
Пример 7. Необходимо построить зависимость между средним временем обработки заявки на информационный поиск (y ) и интервалом между поступлениями заявок (x1 ), интервалом обслуживания заявок (x2 ) для примера 5.
Проводится имитационный эксперимент: при различных значениях x1 , x2 имитируется обработка заданного числа заявок и вычисляется среднее значение y при каждом прогоне имитационной модели (при заданных на определенном уровне значениях x1 , x2). В результате получается выборка исходных данных, по которой оцениваются параметры модели вида (21.8.).
Построенную модель далее можно использовать для оценки среднего времени обслуживания информационного запроса при заданных входных переменных с некоторой вероятностью р.
Достоинства и недостатки применения вероятностно-статистических методов такие же, как и у имитационных методов моделирования.
Разработано обширное прикладное статистическое программное обеспечение, в котором реализованы вероятностно-статистические методы, например, пакеты Statistica, SPSS, StatGraphs и многие другие.
| ← 21.1. Математическая модель системы (объекта) | 21.3. Технология математического... → |
