Главная страница / 20. Классификация и формы представления ...: 20.1. Формы представления...
20.1. Формы представления моделей
| ← 19.2. Контрольные вопросы и задания | 20.2. Классификация математических моделей → |
В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим, точно таким же [6]. При моделировании абсолютное подобие не имеет места и нужно стремиться к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объекта.
В основу классификации видов моделирования можно положить разные классификационные признаки [6–8],[10–17].
В зависимости от формы представления объекта (системы) можно выделить [11,12]:
- мысленные (абстрактные) модели;
- материальные (реальные) модели.
Классификация моделей в зависимости от формы представления приведена на рис. 20.1.
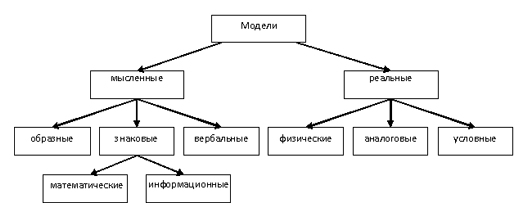
Рис. 20.1. Классификация моделей по форме представления
Материальные модели воспроизводят физические, геометрические и другие свойства объектов в материальной форме. Материальная модель может быть похожей копией объекта, выполненной из другого материала, в другом масштабе, с отсутствием ряда деталей. Строятся реальные модели средствами материального мира.
В свою очередь материальные модели подразделяются на физические, аналоговые и условные модели [12].
При построении физических моделей подобие между оригиналом и моделью устанавливается в результате физического взаимодействия (прямое подобие). Отличительной особенностью физической модели является то, что она в некотором смысле «выглядит» подобно моделируемому объекту.
Примеры физических моделей: фотография, модель самолета, игрушечный кораблик, домик из кубиков, модель кристаллической решетки, макет здания, копия произведения искусства. Физические модели могут иметь вид полномасштабных объектов (например, тренажеры), выполняться в уменьшенном масштабе (например, модель солнечной системы, глобус) или в увеличенном масштабе (например, модель атома).
Аналоговая модель – модель, в которой свойство реального объекта представляется некоторым другим свойством аналогичного по поведению объекта. При построении аналоговых моделей используется косвенное подобие.
Примеры аналоговых моделей: электрический ток в подходящих цепях может отображать поток товаров в некоторой системе; логарифмическая линейка, в которой количественные характеристики некоторого объекта представлены отрезками шкалы в логарифмическом масштабе; часы – аналог времени; автопилот – аналог летчика; подопытные животные у медиков – аналоги человеческого организма.
Условные модели – модели, подобие которых оригиналу устанавливается в результате соглашения (условное подобие).
Примеры условных моделей: деньги (модель стоимости); удостоверение личности (официальная модель владельца); разнообразные сигналы (модели сообщения); рабочие чертежи (модели будущей продукции); карты (модели местности) и т.д.
Модель может отображать реальность более абстрактно – словесным описанием в свободной форме, описанием, формализованным по каким-то правилам, математическими соотношениями и т.п. Будем называть такие модели мысленными (абстрактными). Абстрактные модели строятся средствами мышления.
При классификации абстрактных моделей выделяют следующие: образные, вербальные, знаковые (математические, информационные).
Образные модели – получены в результате раздумий, умозаключений.
Например, наше поведение при переходе улицы. Человек анализирует ситуацию на дороге и вырабатывает свою модель поведения. Или музыкальная тема, промелькнувшая в голове у композитора, рифма – пока еще в сознании поэта.
Вербальные (словесные и текстовые) модели. Эти модели используют последовательности предложений на формализованных диалектах естественного языка для описания той или иной области действительности (примеры такого рода моделей: милицейский протокол, правила дорожного движения, нотный текст, стихотворение).
Знаковая модель описывает моделируемую систему с помощью условных знаков, символов, в частности, в виде математических, физических и химических формул. Наиболее мощные и развитые классы знаковых моделей представляют собой математические и информационные модели.
Математическая модель – это искусственно созданный объект в виде математических, знаковых формул, который отображает и воспроизводит структуру, свойства, взаимосвязи и взаимоотношения элементов исследуемого объекта.
Например, математическая модель звезды будет представлять собой сложную систему уравнений, описывающих физические процессы, происходящие в недрах звезды. Другой пример математической модели – математические соотношения, позволяющие рассчитать оптимальный (наилучший с экономической точки зрения) план работы какого-либо предприятия.
Приведем несколько определений информационной модели, данных разными авторами.
Информационная модель [3] – модель объекта, представленная в виде информации, описывающей существенные для данного рассмотрения параметры и переменные объекта, связи между ними, входы и выходы объекта и позволяющая путем подачи на модель информации об изменениях входных величин моделировать возможные состояния объекта.
Информационная модель [16] – совокупность информации, характеризующая существенные свойства и состояния объекта, процесса, явления, а также взаимосвязь с внешним миром.
Информационные модели [11,14] – класс знаковых моделей, описывающих информационные процессы (получение, передачу, обработку, хранение и использование информации) в системах самой разнообразной природы.
Примерами таких моделей могут служить OSI – семиуровневая модель взаимодействия открытых систем в компьютерных сетях, или машина Тьюринга – универсальная алгоритмическая модель.
Подчеркнем, что приведенная классификация лишь одна из многих, граница между видами моделей, их иерархия может быть представлена весьма условно. Например, в ряде литературных источников [13,16] понятие «информационная модель» рассматривают более широко и делят все модели на материальные и информационные. В основе такого подхода лежит расширительное толкование понятия «информация»: «Информацией является почти все на свете, а может быть, даже вообще все». Такой подход не вполне оправдан, так как он переносит информационную природу познания на суть используемых в процессе моделей – при этом любая модель является информационной [11].
Существует подход, при котором информационные модели относят к подклассу математических моделей. Однако в рамках информатики как самостоятельной науки, отдельной от математики, физики, лингвистики и других наук, выделение класса информационных моделей представляется целесообразным [11].
Далее остановимся более подробно на классификации математических моделей, так как именно этот класс моделей широко применяется при решении практических задач.
| ← 19.2. Контрольные вопросы и задания | 20.2. Классификация математических моделей → |
